Quan comptar no és només sumar: comprendre el significat dels nombres

Hi ha una idea fonamental que sovint oblidem a l’aula: com més complex és un concepte matemàtic, més temps i dedicació cal per comprendre’l realment. Això, que pot semblar una obvietat, entra en conflicte amb l’estructura del currículum, el ritme dels cursos i la pressió per “avançar temari”.

Però si volem que els nostres alumnes entenguin les matemàtiques com una eina per pensar millor, cal fer una pausa i tornar a les preguntes essencials. Què vol dir comprendre els nombres i les operacions?

Fer bones preguntes per construir significat

El bloc de “Nombres i operacions” és sovint un territori mecànic. Els alumnes aprenen a sumar, restar, multiplicar i dividir, però… què entenen realment del que estan fent? Què sabran fer amb aquests coneixements fora d’una "fitxa"?
Aquí tens algunes preguntes que poden ajudar a orientar l’aprenentatge i donar-li sentit:

• Quina informació transmeten els nombres?
• Com afecta la posició d’un dígit en un nombre al seu valor?
• De quina manera es poden agrupar els elements d’un conjunt?
• Quines preguntes es poden respondre amb la suma o la divisió?
• Com es relacionen les quatre operacions entre si?
• Quines estratègies tenim per fer una estimació raonable?
• Quines eines de càlcul són més útils segons la situació?
• Quin tipus de problemes podem respondre amb cada operació?

Aquest tipus de preguntes ajuden a anar més enllà de la tècnica. Ens obren la porta a una comprensió més profunda, a connexions amb altres idees i, sobretot, a la capacitat de transferir el coneixement a situacions reals.

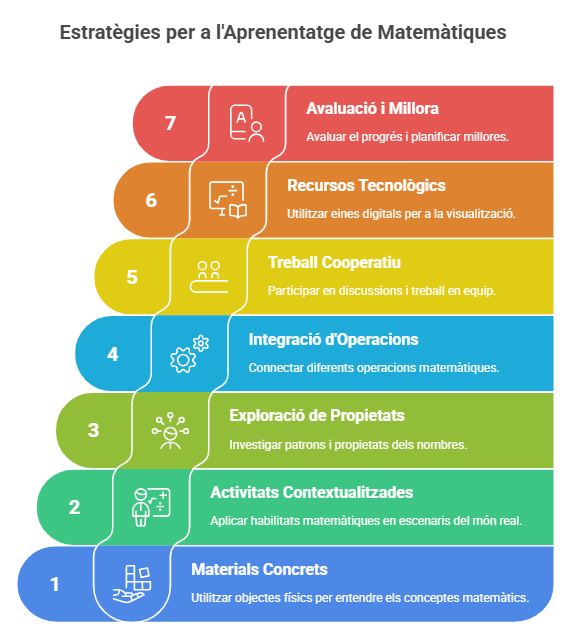
Estratègies per fer-ho possible

• Perquè els alumnes puguin respondre aquestes preguntes, cal crear escenaris d’aprenentatge rics i donar-los temps per explorar, equivocar-se i construir sentit. Algunes propostes clau:
• Treballar els conceptes amb materials concrets i aplicacions pràctiques. Quan poden tocar, moure, representar i veure els nombres en acció, els fan seus.
• Crear activitats en què calgui comptar, agrupar, estimar i comparar. No com a exercicis aïllats, sinó dins de projectes o problemes contextualitzats. Recordant sempre que el concepte de context és molt més extens que el normalment es transmet.
• Explorar les propietats dels nombres anant més enllà de la repetició i entrant en la pràctica productiva: buscar patrons, formular conjectures, representar idees de maneres diverses.
• Integrar les operacions entre si, no com compartiments estancs sinó com eines que es relacionen i que es poden aplicar en múltiples contextos.
• Afavorir el treball cooperatiu i les discussions. Quan expliquen el que pensen, quan contrasten idees, construeixen comprensió.
• Fer servir recursos tecnològics que permetin representar, experimentar, jugar i visualitzar els conceptes des d’altres angles.
• Fer revisions periòdiques i establir plans de millora. Entendre què sap fer cada alumne, i ajudar-lo a avançar des d’allà on és.

Comprendre abans que repetir

Les matemàtiques són una manera de mirar el món. Quan els alumnes entenen com funcionen els nombres, què vol dir dividir o per què cal estimar, guanyen eines per pensar millor. No es tracta només d’aprendre a fer comptes, sinó d’entendre els fonaments que sostenen aquestes operacions.

I per això cal temps. Cal fer bones preguntes. Cal crear espais on puguin experimentar, parlar i equivocar-se. I cal que, com a docents, ens preguntem també nosaltres: quina mena de comprensió vull que construeixin els meus alumnes?Quan entenem que aprendre matemàtiques no és només dominar tècniques, sinó comprendre idees i fer-les servir per prendre decisions i resoldre situacions, deixem de parlar d’una assignatura i comencem a parlar d’un llenguatge per entendre el món.

Sobre la numeració i el càlcul també podeu consultar:

Idees rellevants de Matemàtiques: Numeració i càlcul